A quadrilateral is a plane figure with four sides or edges and four vertices or corners. Quadrilaterals can be regular and defined shapes with four sides: rectangles, squares, trapezoids, kites, or irregular and undefined shapes.
While a circle is a closed two-dimensional object in which all points in the plane are equidistant from a single point known as the “center.” The line of reflection symmetry is formed by every line that travels through the circle. For any angle, it also exhibits rotational symmetry around the center.
Quadrilaterals Inscribed Within Circles
A quadrilateral inscribed in a circle is a quadrilateral with four vertices on the circumference of a circle, also known as a cyclic quadrilateral or chordal quadrilateral in geometry. The chords of the circle are the quadrilateral’s four sides in a quadrilateral inscribed circle.
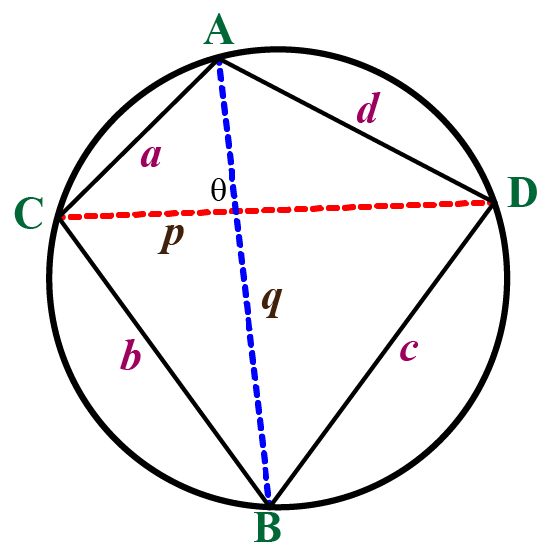
The circumcircle or circumscribed circle is a circle that contains all of the vertices of any polygon on its circumference. A cyclic quadrilateral is one in which all four vertices of a quadrilateral lie on the circle’s circumference. In other words, the vertices of a cyclic quadrilateral are formed by joining any four locations on the circumference of a circle.
It can be imagined as a quadrilateral inscribed in a circle, with all four vertices of the quadrilateral lying on the circle’s circumference. Not every quadrilateral is cyclic, but you can think of a handful. Because a circle may be drawn around it, touching all four vertices, every rectangle, including the particular case of a square, is a cyclic quadrilateral. Non-rectangular parallelograms, on the other hand, are not cyclic.
What are the Properties of Cyclic Quadrilaterals?
There’s no method to create a circle around a non-rectangular parallelogram that touches all four of its vertices. Below is the enumeration of properties of a cyclic quadrilateral.
- A quadrilateral inscribed in a circle has all four vertices on the circle’s circumference.
- In a cyclic quadrilateral, the sum or total of the two opposite angles equals 180 degrees (supplementary angles).
- An exterior angle’s length is equal to the length of the opposite internal angle.
- The Cyclic quadrilateral theorem is used to calculate the ratio between the diagonals and the sides. The product of the diagonals of a quadrilateral inscribed in a circle is equal to the total of the product of its two pairs of opposite sides.
- At the center of the circle, the perpendicular bisectors of the four sides of the inscribed quadrilateral intersect.
Cyclic quadrilaterals are useful in a variety of geometry problems, especially ones that require angle chasing. It’s not uncommon, for example, to add points (and lines) to diagrams to take advantage of the features of cyclic quadrilaterals.
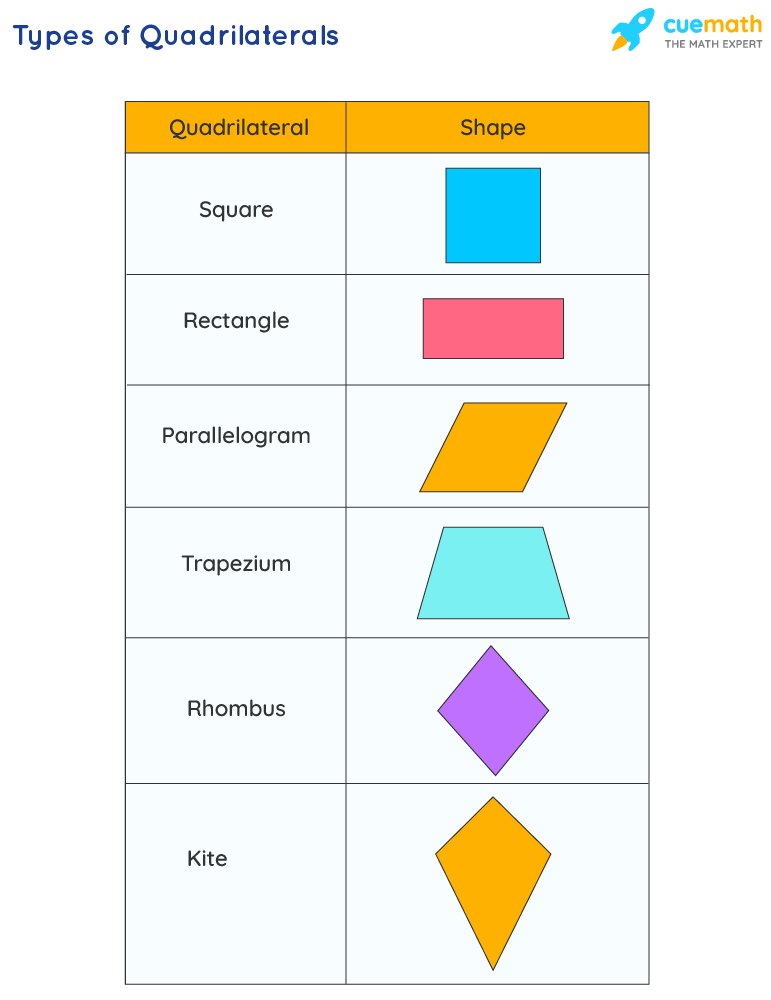
A quadrilateral is a four-sided polygon with four finite line segments on each side. The word quadrilateral is made up of two Latin words: “Quadri”, which means four, and “Latus”, which means side. It’s a two-dimensional figure with four vertices and four sides (or edges). Quadrilaterals come in a variety of shapes and sizes. All of these quadrilaterals have four sides, and the sum of their angles is 360 degrees since the term quad means four.
The perimeter of a two-dimensional shape is the total distance covered by its boundaries. Because we know that a quadrilateral has four sides, the perimeter of every quadrilateral is equal to the sum of all four sides’ lengths. The number of unit squares that can fit into a quadrilateral is the area of the quadrilateral. The area of a quadrilateral varies depending on the quadrilateral.
Each of the quadrilaterals has its unique set of characteristics. There are, nevertheless, some qualities that all quadrilaterals share. There are four sides to them. They are made up of four vertices and are divided into two diagonals.
360° is the sum of all interior angles. If you want to learn all the properties of the quadrilateral, then refer to Cuemath. It educates you with all the properties and essential characteristics of every topic. It also gives you a brief introduction to the topic. There are very few chances of you getting stuck anywhere.